Scoring and Normalization
Introduction
The Relevance Module assesses which segment best describes the visitor. It combines the characteristics of a segment with the scores provided by the Scorer to assign a score to each segment.
This document describes the steps in which request data is processed and the rationale behind the process.
Ingredients
Scoring
A scorer assigns a value between 0 and 1 to each target group in the configuration. For each characteristic, a different scorer can be used. This makes it possible to use an appropriate targeting data type, target group configuration, and scoring. The value 0 has the interpretation "no match", value 1 can be interpreted as "perfect match".
We will denote the value for target group X and visitor V as Value[ X, V ]. I.e. X might be 'Amsterdam' and V is a particular visitor.
Segment Expression
A segment expression is a formula that is used to combine scores for different target groups into a single number. It represents a user-visible sentence such as
"An 'Urban Sunbather' is someone who comes from Amsterdam, and the weather is Sunny"
as
RawScore['Urban Sunbather', V] := Value['Amsterdam', V] * Value['Sunny', V]
where Value[ X, V is the value assigned to target group X by its score for visitor V. Note that each Value is a real number between 0 and 1, inclusive. Which values are actually returned depends on the scoring engine for the characteristic. Some scoring engines return any value between 0 and 1, some only return either 0 or 1 : In case of the weather, we assume 0 is no sun at all, 1 is sunny, and any value between 0 and 1 represents partially sunny. In case of the location, we assume a value of either 0 or 1 and nothing in between (let's not start a theoretical Heisenberg discussion here)
Normalization
Scores of different segments need to be normalized to be able to compare them. The guiding principle here is that
facts that happen
less frequently
are
more important
when they happen
Assume that the average raw score for an Urban Sunbather is, very low, let's say 0.08. I.e. most visitors are either [not from Amsterdam], visit the site when it's [not Sunny], or [both]. Then when a visitor arrives that does have a low raw score , say 0.24, then for that visitor, the Urban Sunbather segment is important, as he scores much higher than average visitors on that segment.
A simple formula that takes these considerations into account is the following
Score['Urban Sunbather', V] = RawScore['Urban Sunbather', V] / AverageRawScore['Urban Sunbather']
where
AverageRawScore['Urban Sunbather'] = Sum[ RawScore['Urban Sunbather', W], W is any visitor ] / # of visitors
In the engine, the average is only calculated over the last # number of visitors. # is by default 1000 : This keeps the averages possible to change even when the average is based on many millions of values. The mathematical term for this is Exponential moving average
One of the properties of this normalization is that it is possible to compare segments that extend each other. Let's introduce a new segment, the Amsterdammer:
"An 'Amsterdammer' is someone who comes from Amsterdam"
So now we have two segments :
-
Urban Sunbather (from Amsterdam and the weather is sunny)
-
Amsterdammer (from Amsterdam)
It is easy to see that the RawScore of the Urban Sunbather can be at most equal to the raw score of the Amsterdammer : when a visitor is from Amsterdam, he has a raw score of 1. Now, Urban Sunbather will only score 1 as well for his raw score when it is completely sunny (the result of the scorer always returning a value between 0 and 1 for Value['Sunny', V].). The normalization will now ensure that the Urban Sunbather segment will get a higher Score than the Amsterdammer when the weather in Amsterdam is more sunny than the average sunnyness in Amsterdam.
Data flow in the Relevance Module
The Relevance Module coordinates the actions of a number of components.
-
(pluggable) collectors inspect the incoming requests and store targeting data for the visitor
-
scorers take this targeting data and calculate scores for each of the configured target groups
-
the segment evaluator takes the segment configuration and combines the target group scores into normalized segment scores
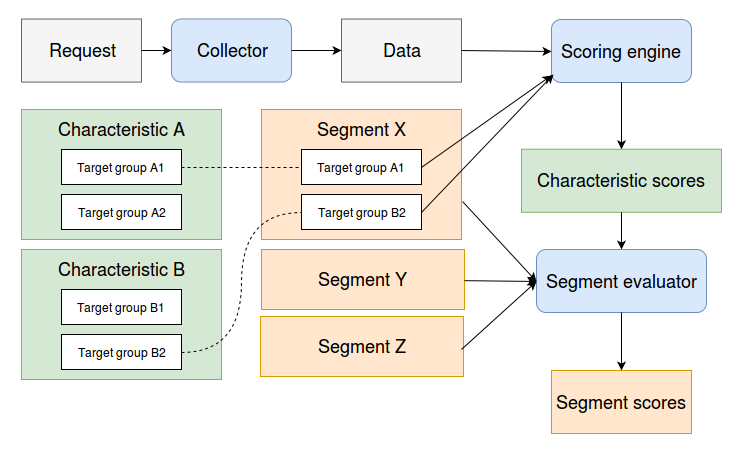
The steps that turn request information into segment scores.
The scoring and normalization are the last parts of the process, integrating the contributions from different target groups.
Example
A worked out example might help illustrate what's going on. Let's assume we have a visitor that is located in Amsterdam on a Reasonably Sunny day:
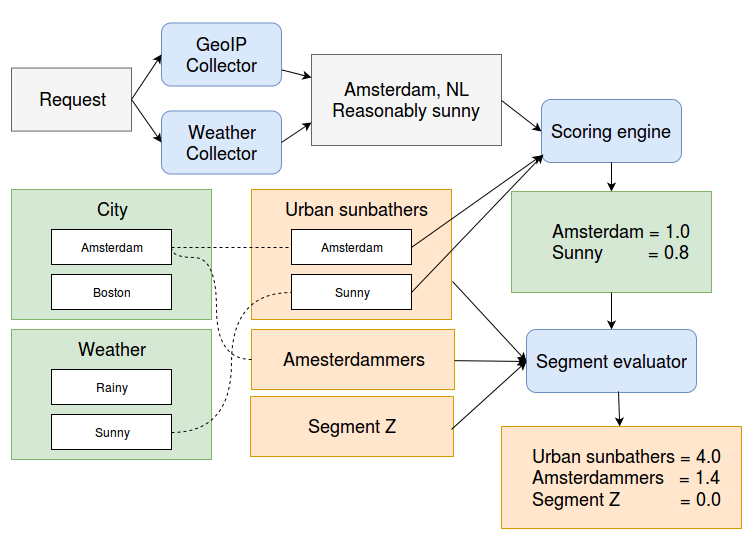
The GeoIPCollector adds the targeting data ' Amsterdam, NL'; the Weather collector adds ' Reasonably Sunny'. The configured target groups include the city of Amsterdam (NL) and Sunny weather. So the scorer assigns the values 1.0 to Amsterdam and 0.8 to Sunny.
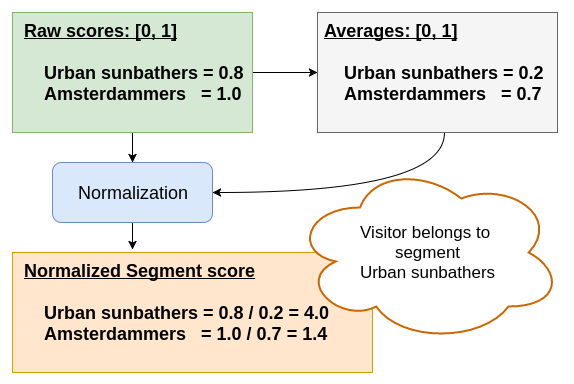
Then, the evaluator processes these numbers. The raw scores for ' Urban Sunbather' and ' Amsterdammer' are 0.8 and 1.0, respectively. As mentioned above, the raw score for Urban Sunbather is always less than that for Amsterdammer.
Now the normalization takes care of providing a suitable boost factor for rare events. Let's say that on average, 70% of the visitors come from Amsterdam, assigning an average of 0.7 to the Amsterdammer segment. Visitors that come from Amsterdam on a sunny day are rare, say 20% (on average Amsterdam is a pretty Cloudy city).
Since our visitor has the good fortune to visit on a Reasonably Sunny day, the Urban Sunbather segment is much more appropriate than the less specific Amsterdammer. This is reflected in the scores of 4.0 versus 1.4.
Fuzzy Boolean Expressions
The segment evaluation is based on the fuzzy logic:
Value[ A ^ B ] := Value[ A ] * Value[ B ]
Value[ A v B ] := Value[ A ] + Value[ B ] - Value[ A ] * Value[ B ]
Value[ ¬ A ] := 1 - Value[ A ]
where Value[ A ] and Value[ B ] are between 0 ("false") and 1 ("true"). It is easily shown that the extremal values implement boolean logic. This system makes it possible to evaluate compound expressions such as
Value[ (A ^ B) v C ]
to
Value[ A ] * Value[ B ] + Value[ C ] - Value[ A ] * Value[ B ] * Value[ C ]
One could attach a probabilistic interpretation, where we equate Value[ A ] with the probability that A is true. Interpreted in this way, the above translation rules correspond to the naive bayesian Ansatz where different variables are assumed to be independent.

